Scatter Plot
Scatter plots (also known as Scatter Diagrams or scattergrams) are used to study possible relationships between two variables (see example in figure 1 below). Although these scatter plots cannot prove that one variable causes a change in the other, they do indicate, where relevant, the existence of a relationship, as well as the strength of that relationship. A scatter plot is composed of a horizontal axis containing the measured values of one variable (independent variable) and a vertical axis representing the measurements of the other variable (dependent variable).
The purpose of the scatter plot is to display what happens to one variable when another variable is changed. The scatter plot is used to test a theory that the two variables are related.
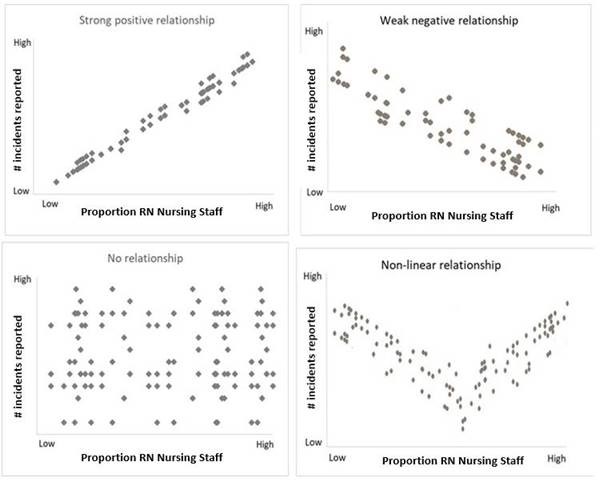
The scatter plot is interpreted by assessing the data: a) Strength (strong, moderate, weak), b) Trend (positive or negative) and c) Shape (Linear, non-linear or none) (see figure 2 below).
A scatter plot could be used to determine if there is a relationship between outside temperature and cases of the common cold? As temperatures drop, do colds increase?
Another example (see image below), is there a relationship between the length of time of a consultation with a doctor in outpatients and the patients level of satisfaction? The closer the points hug together the more closely there is a one to one relationship.
The statistical test to use to test the strength of the relationship is Pearson's Correlation Coefficient, also known as Pearson's r.
To learn more about Scatter Plots please watch this short educational video.
Scatter plot video
- Scatter Plot Template XLS ~569KB
Figure 1: Example Scatter Plot
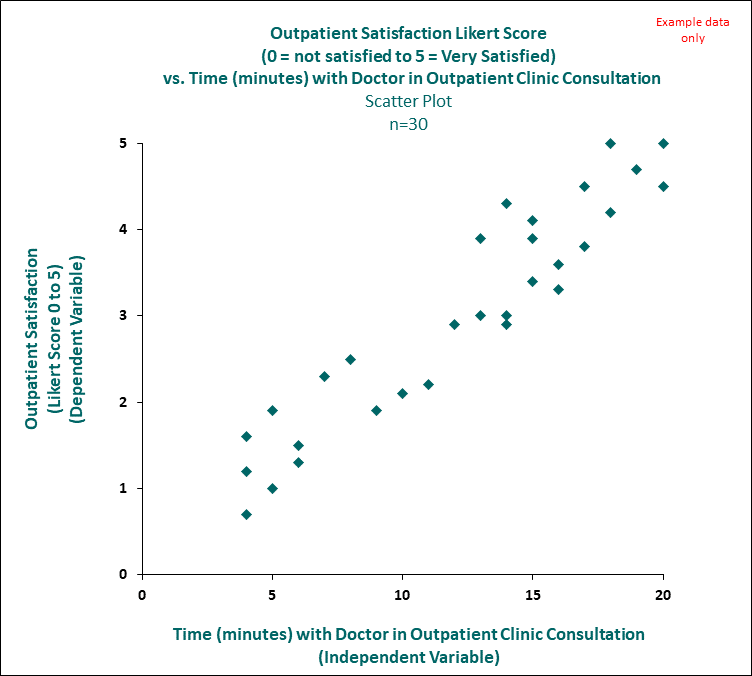
Figure 2: Interpretation of a Scatter Plot
Feedback
Was this quality tool web page useful? Do you have suggestions on how we might make it even better?
Please provide us with your feedback via this short evaluation survey.
